Chaos Project(page3)

ICMS

Page:

Phase Space Portraits

In studying dynamical systems, it is often helpful to have a qualitative idea of how the system evolves from one state to the next. The evolution is studied using a phase diagram. The dimensions of a phase diagram are decided by the number of variables required to specify the state of the system. Each point in phase space (the mathematical space in which phase diagrams are constructed) represents a state of the system, and as the system evolves, it traces out a trajectory in phase space.

For example, the phase diagram of a simple pendulum with initial displacement, q , is shown. The arrow signifies the direction of flow of time. The values of q and dq /dt specify a unique state, so the phase space is two-dimensional.

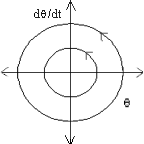
chaos2_1.gif (3126 bytes)

Typically a 2-D phase space can have a combination of the following features:

After a system returns a state it cannot follow a different path. So trajectories in phase space cannot intersect.

Poincare Sections

Another technique used for studying dynamical systems is a Poincare section. Here, instead of marking every point in the trajectory in the phase-space diagram, every time a certain event occurs a point is marked in phase-space. For example a Poincare section of a planet could involve its position and momentum at successive perihelions. A periodic trajectory would involve the system returning to its original state, after which it would evolve in an identical fashion. This means that the same points would be marked over and over again on the Poincare section. On the other hand, in a chaotic system the same state would never recur, and so we would get an unrelated scatter of points. The Poincare section of Hyperion on the facing page demonstrates both these phenomena.

Attractors

An attractor, as the name suggests, is a feature in phase space which attracts nearby trajectories. From the diagrams it is clear that single points and stable limit cycles are the only attractors in 2-D phase space. So an attractor in 2-D phase space would either drive nearby trajectories to a stable point or to a limit cycle (where the trajectory would become periodic). In both cases, henceforth, the system would become predictable. Attractors which do neither of these are generally called strange attractors. These are the kinds of attractors which chaotic systems usually have. So it is evident that chaotic attractors exist only in phase spaces of dimension greater than 2.