|

Random systems form the other end of the spectrum. If a blindfolded person is asked to pick a ball from a bag full of different coloured balls, there are no laws to tell us which colour will be chosen. The system is random, and also unpredictable. To understand the difference between Randomness and Chaos better, consider the iterative function:
Xn+1 º 2Xn (mod 1)
There is no element of "randomness" or "unpredictability" in the values of Xn for successive n. But the values are highly sensitive to initial conditions, the mod operation serving to introduce the non-linearity.
In the graph below, the blue line corresponds to initial value X0=0.0049 and red line to X0=0.0050. The two initial values differ only in the fourth place of decimal, but the values follow completely different paths after 10 iterations.
Note that a physical quantity, which varies chaotically, may be governed by a very simple expression, as above.
A Change in Philosophy
The fact that many systems behave in a chaotic manner has important consequences, both for the way physics is done and for the philosophy underlying physics. Physical laws have, for long, been associated with complete predictability. Newton felt that he had discovered laws that caused the world to evolve in a completely predictable, clockwork fashion. The universe was associated with complete order and regularity. Quantum theory had introduced the notion of a probabilistic interpretation of physical laws, but people still associated classical systems with completely predictability. The theory of chaos shattered this belief by showing that even in the classical realm, predictability is often unattainable. This unpredictability extends to most systems around us.
A dramatic example is that of the weather. In fact the revival of interest in chaotic phenomena, after the long neglected work of Poincare, began with the celebrated paper of Edward Lorenz, a meteorologist. Working with an idealized model of the atmosphere, he showed that weather conditions could be highly sensitive to small perturbations. Putting it dramatically "A butterfly flapping its wings in China may cause a tornado in Brazil!"
Chaos theory has also yielded insights in fields such as fluid dynamics, where the concept of strange attractors has been used to explain turbulence. Apart from Physics, chaos has also found applications in subjects such as cryptography and biology.
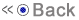
Copyright © 2022 ICICI Centre for Mathematical Sciences
All rights reserved. Send us your suggestions at
|