|
Link We next look at the curves formed by the edges of the ribbon. Note that the twists in the ribbon force these curves to be linked, that is, it is impossible to separate the two curves without cutting one of them. The link is just the number of ways (with orientation) in which one curve loops around the other.
Writhe The third way in which we analyse the ribbon is to look at the axis of the ribbon- the line that bisects the ribbon.
Writhe is the quantity associated with this axis. Writhe measures the non-planarity of the axis of the ribbon. If the axis is planar, then the writhe is always 0. Hence, when the writhe is non-zero, the axis is non-planar.
Whites Formula Link is a topological invariant. It remains unaltered even if the two curves are deformed in space as long as neither is cut. Twist and writhe are geometric quantities. Their values change if the ribbon is deformed in space. Each of link, twist and writhe can be either positive or negative. Link is always an integer whereas Twist and Writhe can take any real values.
These three quantities associated with the ribbon- link, twist and writhe are related by the formula, discovered by James H. White, which is:
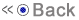
Copyright © 2022 ICICI Centre for Mathematical Sciences |
