|

ELLIPTIC CURVES
The additive group of an elliptic curve
A curve whose equation is y2 = x3 + ax + b is called an elliptic curve. Its graph looks like:

There is a nice method of "adding" two points on an elliptic curve to get another point on it. To add the points P and Q, draw the line through them and see where it cuts the curve again. Reflect that point in the x-axis. The result is defined as the sum of these points and written as P + Q.
If P(x,y) lies on the curve, it is immediate that Q(x,-y) also lies on it. There is no other point on the curve whose abscissa is x. To define the sum of these two points, we imagine a point O at infinity through which every vertical line passes. Then it is obvious that for every point P on the curve,
O + P = P + O = P
Note that the points P and Q mentioned in the paragraph above have the property that
Q + P = P + Q = O
2P is the reflection of the point where the tangent at P cuts the curve. Note that any line cuts the curve in at most three points. It is easily checked that the points on the curve form an abelian group under the addition defined above.
Elliptic curves over finite fields
The elliptic curve described on the left is over the real numbers. Similarly, an elliptic curve over a finite field F is defined as the (finite) set of points (x,y) which satisfy the equation y2 = x3 + ax + b where x, y, a and b belong to F.
Using the equation of the line joining two points, their coordinates and the equation of the elliptic curve, the coordinates of the sum of two points can easily be calculated. These equations motivate the definition of addition of points lying on an elliptic curve over a finite field.
If P=(x1,y1) and Q=(x2,y2), then P + Q = (x3,y3) where:
The coordinates of 2P are given by:
Example: Consider the elliptic curve y2 = x3 over the finite field F11. There are 12 points lying on this curve.
If P = (3, 4) & Q = (4, 8), then P + Q = (9, 5).
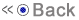
Copyright © 2022 ICICI Centre for Mathematical Sciences
All rights reserved. Send us your suggestions at
|