The Art of Computer Graphics

ICMS

Page:

Rotation

Rotation is used either to rotate an object to see it from a new angle, or to generate a surface of revolution by rotating a curve about a line.

We are rotating the given curve about the x-axis in the diagram given above.

The rotation matrix for rotation of a point about the x-axis by an angle q is

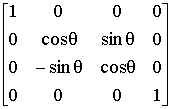
wpe8.jpg (3588 bytes)

Scaling

wpe4.jpg (2249 bytes)

Squeezing or stretching an image, without altering its basic shape, is called scaling. The surface generated by rotating the curve is then scaled to required proportions.

If S_x, S_y, S_z are the scaling factors along the x, y and z axes respectively, then the scaling matrix is

wpe9.jpg (3148 bytes)

Translation

wpe5.jpg (2353 bytes)

Moving an object to a new position in space is known as translation.

The scaled surface is translated to the desired position on the screen.

If T_x, T_y, T_z are the displacements along the x, y and z axes respectively, then the translation matrix is

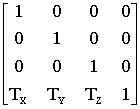
wpeA.jpg (2942 bytes)

Perspective Plotting

As the viewing surface is only two-dimensional, we must have some way of projecting our three-dimensional object onto a two-dimensional screen.

In perspective projection, the lines of projection converge at a point called the centre of projection. All the pictures in this panel have been produced through perspective plotting.

If the centre of projection is (x_c,, y_c, z_c) then the matrix for perspective projection is

wpeB.jpg (3820 bytes)

Note that the point (x, y, z) is being represented as the point (x, y, z, 1) in four-dimensional space. So all our `transformation' matrices are 4 ´ 4 matrices. On post-multiplying (x, y, z, 1) by a `transformation' matrix we can find the new co-ordinates.