THE TRANSPORTATION PROBLEM

Suppose an oil company has five refineries and has to distribute production to fifty demand points. How should it allocate production from each of the refineries to each of the demand points so that the cost of distribution is minimized?

The same general problem is faced in many industries with several production locations and dispersed buyers. SAIL, for example, has plants at Bokaro, Rourkela etc., and it supplies steel to the railways, shipping and automobile and other industries all over India.

These are all examples of what is known as the Transportation Problem. In a typical problem of this kind, a firm has a given number of supply points or factories (called origins), each of which can produce a known amount. It has to supply to buyers at different locations (called destinations), and the amounts that have to be sent to each destination are also known. The costs of transporting one unit of the good from each origin to each destination are given. The problem is to devise a transportation schedule (which factory supplies how much to which destination) that meets the demand at each destination at the lowest possible distribution cost.

A related problem is the transshipment problem, in which any shipping or receiving point (origin or destination) may also act as an intermediate point for onward transmission. Another related problem is that of maximal flows in networks.

Mathematical statement

We have m supply points O₁, & , O_m, and n demand points D₁, & , D_n such that:

• The i^th supply point can supply an amount s_i.
• The j^th destination requires an amount d_j.

• The cost of transporting one unit from O_i to D_j is c_ij.

Let x_ij be the amount transported from O_i to D_j. Then the total transport cost incurred is å _i,j c_ijx_ij, and the transportation problem is to find x_ij so as to

Mathematically, therefore, the problem is one of minimizing a linear function (of the mn variables x_ij) subject to linear equality and inequality constraints.

LINEAR PROGRAMMING

In the general Linear Programming (LP) Problem, a linear objective function has to be optimized (either maximized or minimized) subject to a set of linear constraints:

A problem of this kind arises, for example, if we wish to maximize revenue from the production of n goods using m different inputs, subject to m main constraints (of resource availability) in addition to n non-negativity constraints, where

x_j = amount produced of good j,

p_j = price of good j,

b_i = amount of i^th resource available,

a_ij = amount of resource i required per unit of output j.

A feasible solution is a vector (x₁ , ... , x_n ) satisfying all the m + n constraints. The feasible set is the set of all feasible solutions; geometrically, this set is a convex polytope.

By introducing m slack variables (t₁ , & , t_m), the system of inequalities can be converted into equalities

a_i1 x₁ + & + a_in x_n + t_i = b_i

Clearly, the t_i must be non-negative and they make no difference to the objective function.

The main constraints form a system of m equations in m + n variables. In general, some n of the variables can be assigned arbitrary values. We set them equal to zero and solve for the remaining variables to obtain a basic solution. The n variables set to zero are called the non-basic variables and the others are called the basic variables. A basic feasible solution is a basic solution in which all the variables are non-negative. Geometrically, a basic feasible solution is a vertex of the feasible set; here at most m variables are non-zero.

An optimal solution is a feasible solution that optimizes the objective function over the feasible set. A problem is infeasible if the feasible set is empty, and is unbounded if there is no upper (lower) limit to the value of the objective function in a maximization (minimization) problem.

It can be shown that if the feasible set is non-empty and bounded, at least one basic feasible solution is the optimal solution. The Simplex Algorithm moves from one basic feasible solution to another, ensuring at each move that the value of the objective function does not decrease. We check for optimality at each stage and stop when we have reached the optimal solution. This method also checks for infeasibility or unboundedness.

For a graphical representation of feasible, infeasible and unbounded sets, and more, see our computer display.

DUALITY RESULTS

Corresponding to any linear programming problem (called the primal), there is a dual problem. The dual of the primal (maximization) problem stated previously is:

If the primal is a maximization problem, the dual is a minimization problem. The number of choice variables in the dual equals the number of constraints in the primal and vice versa. The matrix of the coefficients of the main constraints in the dual is the transpose of the corresponding matrix in the primal. It is obvious that the dual of the dual is the primal.

Duality Theorems

A feasible value of a linear programming problem is the value of the objective function for some feasible solution. The fundamental duality results are as follows:

1. Any feasible value of a maximization (primal) problem is less than or equal to any feasible value of its dual problem.
2. If both problems are feasible, both have optimal solutions. If either the primal or the dual has an optimal solution, then so will the other. Also the optimized values of the objective functions of the two problems are equal (max z = min z*).
3. If either problem is unbounded, the other is infeasible. It is possible for both the primal and the dual to be infeasible.
4. As with the primal, the main inequality constraints in the dual can be converted into equalities by introducing slack variables r₁, & , r_n. Then the choice variables for one problem and the slack variables of the other exhibit complementary slackness:

x_j ¹ 0 Þ r_j = 0 ; j = 1, & , n & y_i ¹ 0 Þ t_i = 0 ; i = 1, & , m.

For the transportation problem, the dual is:

The choice variables u_i and v_j can be interpreted as artificial cost variables. If a transporter offers to buy the goods produced at the origin i at price u_i, and sell them back to you at destination j at price v_j, then effectively the transportation cost for you is v_{j - ui. On the other hand, you would have incurred a cost of cij had you transported the good yourself. Therefore you will take up the offer only if vj - ui £ cij.}

Solving the Transportation Problem

Note first that, although there are m + n constraint equations in the mn variables x_ij, because of the balance condition å s_i = å d_j , there are only m + n - 1 independent equations. So the minimum solution requires at most m + n - 1 non-zero x_ij. It is also easy to prove that if the s_i and d_j are non-negative integers, then every basic feasible solution has integral values; also that a basic solution always has a triangular matrix structure.

As an LP problem, the transportation problem can be solved using the simplex algorithm, but in most applications the size of the problem is very large. Fortunately, the special structure of the problem and duality considerations can be exploited to develop a computationally more efficient algorithm.

We begin by finding an initial basic feasible solution using the north-west corner rule (other methods are column minimum, row minimum, and matrix minimum). Consider the following example:

The s_i are the amounts that the origins O_i can supply, the d_j are the amounts the destinations D_j require, and the figures in brackets (in red) are the costs c_ij.

1. Start with the cell in the upper left-hand corner.
2. Set x₁₁ = min [s₁, d₁]. Here, x₁₁ = min [25,40] = 25.
3. If s₁ < d₁ (as is the case here), set s'₁ = 0, and d'₁ = d₁ - s₁ [s'₁ = 0, d'₁ = 40 - 25 = 15]. Then move one cell down and set x₂₁ = min [ s_2, d'₁ ] [x₂₁ = min [45, 15] = 15].

   	D1	D2	D3	D4	si
   O1	(2) 25	(4) 0	(1) 0	(3) 0	0
   O2	(5) 15	(3) 0	(2) 0	(2) 0	45
   O3	(1) 0	(2) 0	(4) 0	(4) 0	26
   dj	40 - 25 = 15	20	16	20	96

4. However if we have not exhausted the supply constraint of the first row (i.e. if s₁ > d₁), set d'₁ = 0, and s'₁ = s_{1 -} d₁. Then move one cell to the right. Set x₁₂ = min [s'₁ , d₂].
5. Continue in this fashion till all your demand and supply constraints get exhausted. Put all remaining x_ij as zero.

You have now reached a basic feasible solution (shown in bold black font in the next panel) which serves as a starting point for the algorithm to find an optimal solution for the transportation problem.

To find an optimal solution

The total transportation cost for the initial basic solution x_ij is Rs 309. We now use an iterative procedure to find an optimal solution, moving from one basic solution to another till we reach an optimal solution which has the lowest possible transportation cost.

Step 1. We set v₁ = 0 and then find the other u_i and v_j using the condition, v_{j -} u_i - c_ij = 0 for all the (shaded) cells corresponding to basic variables. Then u₁ = v_{1 -} c₁₁ = - c₁₁. Similarly as v_{1 -} u₂ = c₂₁, we can obtain u₂. Continuing in this fashion, we get the values for all the u_i and v_j.

 

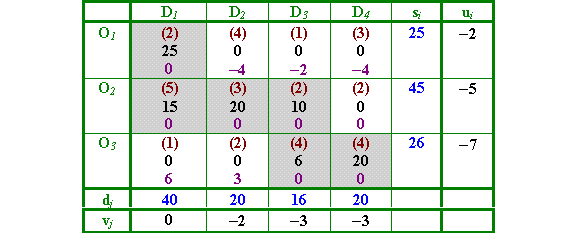
Step 2. For the cells not corresponding to the basic variables we calculate a_ij using the formula v_j - u_i - c_ij = a_ij. (in violet).

In the example, a₁₂ = v₂ - u₁ - c₁₂ = - 2 - (- 2) - 4 = - 4 ,

a₁₃ = v₃ - u₁ - c₁₃ = - 3 - (- 2) - 1 = - 2 and so on.

 

Step 3. If none of the a_ij is positive, we have attained an optimal solution.

If any of the a_ij is positive, select the cell (shaded green) with the largest a_ij. The x_ij corresponding to this cell will enter the next basis. Taking this cell (called the entering cell) form a directed loop.

A directed loop is a closed loop, which connects the entering cell (which has the highest a_ij) with cells already in the basic solution, such that the branches of the loop are orthogonal to each other and such that no cell appears twice.

A directed loop is shown in the table below.

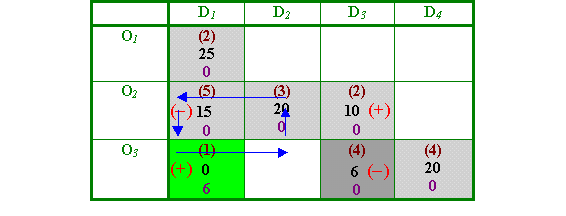
Step 4. Label the entering cell (+), and successive cells in the directed loop alternately (- ) and (+). Amongst the cells labelled (- ), choose the cell with the smallest x_ij. This will be the leaving cell (shaded dark gray).

Step 5. Allocate the x_ij of the leaving cell to the entering cell. The values of each of the x_ij in the directed loop are then changed in the following manner: subtract x_ij (of the leaving cell) from all the cells labelled (- ) in the directed loop and add the same to all the cells labelled (+). We move to a new basic feasible solution, with lower transportation costs.

Return to Step 1.

In the next basic feasible solution, the value of x₃₃ = 6 is transferred from the leaving cell to the entering cell. The other cells in the loop change as follows: x₂₁ = 15 - 6 = 9 and x₂₃ = 10 + 6 = 16.

Our new table is:

The transportation cost is now reduced to Rs. 273.

We continue in this manner till we obtain a table where the a_ij. become non-positive. This final table shows the optimal solution. ( represented below)

 

 

The minimum transportation cost is Rs. 175.

The shaded cells represent routes that are used in the optimal solution; quantities transported along each route are shown in the centre of the shaded cells in black.

The Transportation Problem was first formulated by F.L. Hitchcock in 1941, and was discussed in detail by the Nobel Laureate T.C. Koopmans in a 1947 paper. The general Linear Programming Problem and the Simplex Method were developed by G.B. Dantzig and his associates in 1947; the linear programming formulation of the transportation problem and associated solution procedure were first given by Dantzig in 1951.

Copyright © 2022 ICICI Centre for Mathematical Sciences
All rights reserved. Send us your suggestions at