The Pricing of Options in Financial Markets

ICMS

THE PRICING OF OPTIONS IN FINANCIAL MARKETS

Importers find fluctuations in foreign exchange rates a hindrance to their operations. They may have signed contracts to buy goods at agreed dollar prices, which are worth signing when the exchange rate is Rs. 36 = $1. If, however, when the payments have to be made the exchange rate has become Rs. 39 = $1, they will sustain losses. One way of insulating themselves against fluctuations of this kind would be to sign simultaneously a forward contract in the foreign exchange market. Such a contract would give the buyer a specified amount of dollars at a specified date in the future, at a set exchange rate that is agreed upon now.

A forward contract commits the user to buying the asset at the future date. Another possibility for the importer is a contract that allows him the option of buying dollars at a pre-determined price (called the strike price) on a specified date (called the expiry date), if it is then profitable to do so.

Such a contract is termed a call option. It gives the buyer the right, but (as opposed to a forward contract) not the obligation, to buy a particular asset. A put option gives the user the right (but again not the obligation) to sell the asset. If the asset is actually bought or sold on the expiry date, we say that the option is exercised. In our example, if the importer has bought a call option for dollars at a strike price of Rs. 36 = $1, and the exchange rate is Rs. 33 = $ 1 on the expiry date, it will pay him not to exercise the option.

Forwards and options are examples of derivative assets - financial assets the values of which are derived from the values of other underlying assets. In 1994, approximately $64,000 billion worth of financial derivatives were traded worldwide. In 1995-96 India's estimated GDP was only $266.5 billion and its defence outlay was $8 billion! Speculation in the markets for derivatives can lead to events such as the spectacular crash of Baring's Bank. Derivatives also serve a useful purpose in allowing hedging - protecting oneself against a specific risk by taking on a new one that offsets the former - as in the example of the importer.

Since the buyer of the option can never make a loss, and might make a profit, the option does not come free. He has to pay a price for it. The key question is: how should the option be valued? What price should the buyer be willing to pay and the seller willing to accept for it?

The most important method of option pricing uses the Black-Scholes formula, developed first in 1973 by Fischer Black and Myron Scholes, and by Robert Merton. It is primarily for their work on valuation of options that Merton and Scholes were awarded the Nobel Prize in Economics in 1997.

The Principle of No Arbitrage

An arbitrage opportunity arises when a guaranteed risk-free profit can be made with a sequence of trades in the market. The principle of no arbitrage assumes that in efficient markets the possibility of making such profits is eliminated.

For example, if the price of a Glaxo India share is Rs. 365 in the National Stock Exchange (NSE) but only RS. 362.25 in the Bombay Stock Exchange (BSE), then (if there are no transaction costs) a sure profit of Rs. 2.75 can be made by buying Glaxo shares in the BSE and selling them in the NSE. The price differential has created an arbitrage opportunity.

Such arbitrage opportunities are rare in competitive markets because individuals would move in immediately and exploit them till they disappeared. In actual fact, in the example above the profit to be made would be much less than Rs. 2.75 per share because of the transactions costs: brokerage fees must be paid to buy and sell shares in the respective exchanges. The remaining price difference, if any, would be wiped out very quickly by the market forces of demand and supply.

The price of a stock follows what is called a stochastic process, i.e. it evolves over time with an element of randomness. For example, the price of a TISCO share will exhibit systematic behaviour over the years, depending on whether the company performs well or poorly. But the day-to-day behaviour of the share price is uncertain. The value of an asset depends on what state of nature prevails; the states of nature are randomly determined.

Price of TISCO shares 1/9/97 to 29/11/97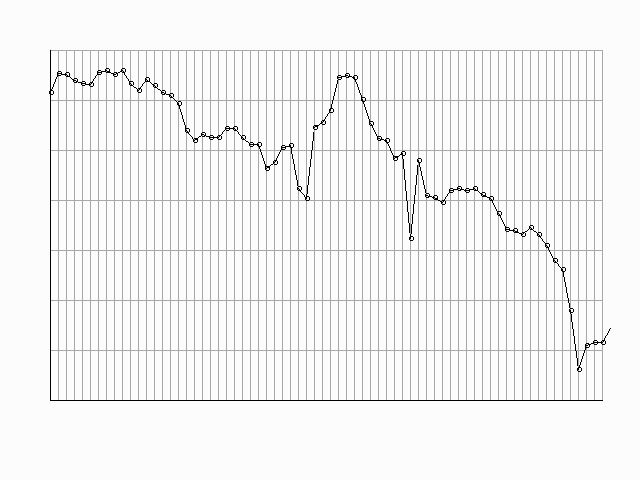

A portfolio is a collection of assets. Since the assets that make up the portfolio have different returns in different states, portfolios too will generate different returns in different states. What an investor ultimately cares about is his final wealth. The "principle of no arbitrage" now tells us that if two portfolios generate the same returns in each state, then they should have the same value to the investor. If this were not so, an arbitrage opportunity arises. If you are holding the more expensive portfolio, sell it and buy the cheaper one. You will end up with a positive sum of money, and a portfolio that generates the same returns.

The Pricing of a Forward Contract

The principle of no arbitrage provides a shortcut to the valuation of derivatives. From the derivatives underlying assets, construct a portfolio that generates the same returns as the derivative in every state of nature. Forming such a portfolio is called a replicating or construction strategy. Then, 'no-arbitrage' implies that the value of the derivative should be the same as that of the portfolio.

Consider first the determination of the forward price of a stock in a futures contract. For simplicity, we assume that this stock pays no dividends. The payoff function for a forward contract is defined as F_T = S_T K, where F_T and S_T are, respectively, the value of the forward contract and the price of the stock on the delivery date, and K is the previously agreed upon forward price. Let F₀ be the value of the forward contract today. The forward price K is set so that no money has to change hands now, that is F₀ = 0.

In the forward contract, at time T you get the value S_T of the stock and you have to make a cash payment of K. We construct a portfolio consisting of the stock and a riskless bond that gives you exactly the same payoff at time T. If you buy one unit of the stock now (which is held till time T) and at the same time sell a bond that promises to pay K at time T, you spend S₀ on the stock and receive the present value K e^-rT for the bond. This portfolio will give you S_T - K at time T, and hence by the no-arbitrage condition should have the same value as the forward contract. Therefore,

K e^-rT - S₀ = F₀ = 0 Þ K = S₀ e^rT .

Thus the forward price K is determined. Notice that the replicating strategy for a forward is a buy-and-hold one.

The Pricing of Options

Valuing a call option is based on a similar idea, and uses the stock and a riskless bond as the underlying assets. However, the replicating strategy for a call option will not be a static buy-and-hold strategy like the one for the forward contract. It will have to be a dynamic strategy in which the composition of the portfolio will change as new information about the price of the stock is received.

We begin by using a binomial tree approach. In this model, the stock price changes at discrete points in time; at each of these times, it can either go up or down to one of two pre-determined values. The stock price, therefore, follows a random walk with drift.

The analysis that follows is for a European option, in which the option can be exercised only on the expiry date. In the American option, the holder is free to exercise the option at any time up to the expiry date, i.e. at any t £ T. In the case of American options, apart from pricing the option, we also have to determine when, if at all, the option should be exercised.

Consider a call option to buy a stock at a pre-determined price K on the expiry date T. You will exercise the option only if the stock price S_T at expiry is greater than the striking price K. Hence the payoff function for an option is

C_T = Max {S_T K, 0}.

Suppose the stock can take only one of two known values at the expiry time. From its starting value S₀, it can either move up to S_u with probability q, or down to S_d with probability (1 q). This can be represented by the tree on the left in Diagram 1.

At time t = 1, the value of the option is C_u = Max {S_u - K, 0} if the stock moves up, and is C_d = Max {S_{d -} K, 0} if the stock moves down.

We must find a construction strategy that replicates the payoff of the derivative with up-contingent value C_u and down-contingent value C_d. We build a portfolio with our two instruments, the stock and the bond. If this portfolio consists of a units of the stock and b of the bond, its initial value is a S₀ + b B (where B is the bond price).

For the payoff from this portfolio to replicate the payoff from the call option we must have a S_u + b RB = C_u after an up move, and a S_d + b RB = C_d after a down move (where R = e^rt is the gross return on the bond after time t). Solving, we get

a = (C_u C_d) / (S_u - S_d) ,

b = 1 ¤ RB [C_{u -} S_u (C_u C_d) / (S_{u -} S_d) ].

If we hold amounts a of the stock and b of the bond, we will have 'synthesized' the derivative. So, by the principle of no arbitrage, the initial market value of the call option should be C₀ = a S₀ +b B. Using the solutions for a and b ,

C₀ = (1/R) [pC_u + (1 p)C_d] ,

where p = (RS₀ S_d) / (S_u S_d). This formula is of the discounted expected value form, with artificial probability p of an up move. Note that p is not the same as the true probability q of an up move. For this probability p (sometimes called the risk-free probability) of an up move, the expected value of stock price next period is RS₀, with present discounted value S₀ - the current stock price.

Now suppose there are two periods of trade. Let C_uu denote the market value of the derivative after two successive up moves, C_ud after an up move followed by a down move, etc. Applying exactly the same reasoning as in the move from t = 0 to t = 1, we have

C_u = (1/R) [ p_uC_uu + (1 p_u)C_ud] and

C_d = (1/R) [ p_dC_du + (1 -p_d)C_dd] ,

where as before p_u = (RS_u - S_ud) ¤ (S_{uu -} S_ud), etc.

Substituting for C_u and C_d in the expression obtained previously for C₀ , we get

C₀ = (1/R²)[ pp_uC_uu + p(1 p_d)C_ud + (1 p)p_uC_du +

(1 p)(1 - p_d)C_dd ].

Thus, from our knowledge of the value of the option in different states of nature at the terminal date, we can work our way back to the value of the option in the preceding period and so on for all the periods. The tree in Diagram 2 illustrates this process of backward induction for three periods.

In the boxes the upper number (in red) is the stock price, and the lower number (in blue) is the option price in the relevant period after a given sequence of up and down moves. It has been supposed that in each period the stock may move up by Rs. 10 with probability q = 0.75, and down by Rs. 10 with probability 0.25. Initial stock price is 100, and for simplicity we have taken R = 1, that is a rate of interest on the bond of 0%. The striking price has been taken to 100. Notice that the "artificial" probability p = 0.5, and the replicating portfolio at t = 0 is to hold 0.5 units of the stock and borrow Rs. 42.5. If the stock price goes up to Rs. 110, the portfolio should be adjusted to 0.75 units of the stock and the borrowing should go up to Rs. 70, and so on.

Option prices in continuous time

It should be evident that after T periods, C₀ can be written as

C₀ = (1/R^T)E_P(C_T) ,

where E_P(C_T) is the expected value of the derivative T periods into the future under the artificial (risk-free) probability measure P. Notice that under the measure P the discounted stock price process S_t is a martingale, that is the conditional expectation of the discounted stock price at any future date, given the price history up to now, is equal to today's stock price. Using properties of martingales, we can then find a construction strategy that replicates the call option. The value of this replicating portfolio is the expectation of the discounted payoff from the derivative under the artificial measure P that makes the discounted stock a martingale. By the no- arbitrage condition the price of the derivative has to be equal to the value of this replicating portfolio.

The binomial procedure works for a discrete-time, discrete-state trading process (in which the stock value jumps only by given amounts at discrete intervals of time). Continuous-time, continuous-state trading can be treated as the limiting case, and the appropriate formula obtained by considering the limit as the number of trading intervals within a given period increases to infinity. Using the Central Limit Theorem, this procedure yields the Black-Scholes option pricing formula. It can be shown that in the limit the stock price process can be represented by an exponential Brownian motion

S_t = S₀ exp(s W_t + mt),

where s is the stock volatility and m is the stock drift. The process W_t is Brownian motion: that is

W_t is continuous with W₀ = 0;
the value of W_t is distributed as a normal random variable N(0,t); and
the increment W_s+t - W_s is distributed as N(0,t) and is independent of the history of what the process did up to time s.

The Black-Scholes option pricing formula is then

C₀ = S₀ F (A) - Ke^{-rT F} (A - s Ö T)

where A = { [ log (S₀ /K) + (r +s ²/2 ) T ] / s Ö T }, F is the cumulative distribution function of the standard normal variate, S₀ is the initial price of stock, r is the riskless rate of return, T is the time to the expiry of the option, and K is the exercise price. Notice that the Black-Scholes formula closely resembles the one for the value of the forward contract, C₀ = S₀ Ke^-rT. The replicating strategy for the forward contract was a buy-and-hold one, whereas the option requires a dynamic strategy, i.e. as the stock price changes, the replicating portfolio constantly changes. This explains the presence of the standard normal cumulative distribution function in the Black-Scholes formula.

Click here for Demo