|

GRAPH THEORY AND THE KÖNIGSBERG BRIDGES
In the 18th century, in the town of KÖnigsberg there were seven bridges that spanned a forked river (the Pregel) that flows past an island. The townsfolk had been vexed by an old puzzle: was there a continuous tour which crossed every one of the seven bridges, but which included no bridge twice? This long-standing problem was solved in 1735 in an ingenious way by the Swiss mathematician Leonhard Euler (1707-1782). His solution, and his generalisation of the problem to an arbitrary number of islands and bridges, gave rise to a very important branch of mathematics called Graph Theory.
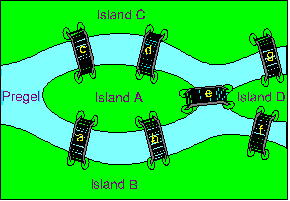
Figure 1
|
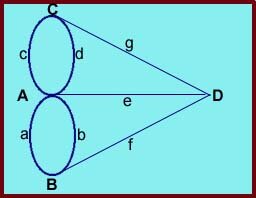
Figure 2
|
Graph Theory
A graph consists of a non-empty set of points (vertices) and a set of lines (edges) connecting the vertices. The number of edges linked to a vertex is called the degree of that vertex. A walk which starts at a vertex, traces each edge exactly once and ends at the starting vertex is called an Euler Trail. If it ends at some other vertex, it is called an open Euler trail. The Königsberg Bridges problem was an attempt to find an open Euler trail. As mentioned in the previous chart,
An open Euler trail is possible if and only if there are exactly two vertices of odd degree. An Euler trail is possible if and only if every vertex is of even degree.
Applications:
Consider a postman who delivers mail in a city. The postman wishes to cover each street in the area at least once and finally return to the post office, travelling the least possible distance. This problem is known as the Chinese Postman Problem (Guan Mei-gu, 1962). Euler trails can be used to find such routes. Further applications of Euler Trails include milk delivery, security guard routing, sweeping roads and even museum or exhibition touring.
Arguably, the most famous result in Graph Theory is the Four-Colour Problem (FCT): Any map on a plane surface (or a sphere) can be coloured with at most four colours so that no two adjacent regions have the same colour. The theorem was proved in 1976, by K.Appel and W.Haken using computers. More recently, P.Seymour announced a simple proof. The FCT has relevance to social geography, for example, in periodic market day analysis (Tinkler, 1973).
Graph Theory has also found uses in Physics (Statistical Mechanics), Probability Theory (Markov chains), Operations Research, Topology, Psychology etc. It is used in the industry for project planning (PERT/CPM), Production Planning and Control (PPC), etc.
Over the course of the last three hundred years, Graph Theory has evolved into a vital branch of mathematics. It is often used as a tool for solving various problems of social and economic importance. The subject has found widespread applications in the areas of computer science, economics, architecture, geography, electrical engineering, modern chemistry, etc.
A SOLUTION TO THE KÖNIGSBERG PROBLEM
Getting back to the problem at hand, we first notice that this puzzle is related to the familiar exercise of trying to trace a given figure on paper without lifting the pencil or retracing a path. The problem can be reduced to a graphical form and then solved with the aid of Graph Theory. In the graphical form, the Königsberg Problem is reduced to studying a set of points and lines (see figure 2).
We begin by assuming that there exists a path (a continuous walk across the seven bridges without re-crossing any bridge) which takes us from a vertex P, the starting point, to a vertex Q, the end point. We also allow for a possibility that P and Q are the same. Since there are more than two vertices, we can choose a vertex V, different from P and Q. We will first cross a bridge connected to V when we walk into V. This is because V is not the starting point. The next bridge will be used when we walk out of V. So, we can eliminate pairs of bridges connected to V. As V is connected to an odd number of bridges, the last bridge will be used for walking into V. This forces V to be the finishing point. This contradicts our hypothesis (Q ¹ V), we have shown that there does not exist a continuous walk satisfying the conditions of the problem.
Similar arguments can be used to show that a graph is traceable if and only if it has either zero or two vertices connected to an odd number of lines. This clearly demonstrates how a seemingly insignificant query can give rise to such a profound concept.
GRAPH THEORY AND PUZZLES
The Queens puzzle:
|
We wish to place as many queens as possible on the chessboard so that no two attack each other. This classic queens puzzle originated with C.F.Gauss (1850) and it was soon found that eight queens were the maximum possible. The Eight Queens problem asks how many solutions exist for the queens puzzle. Gauss showed that there were 92 solutions. In 1910, G.Bennett proved that there are only twelve distinct solutions to the queens problem (i.e. solutions which cant be obtained from each other by rotation or reflection of the chessboard). Look at fig. 1 for one of the solutions
|
|
|
The Knights Tour puzzle:
Knight must tour the chessboard using only legal moves and land on every square exactly once. Look at fig. 2 for one of the answers. The numbers represent the sequence of moves.
|
| 64 |
43
|
62 |
59 |
2
|
27 |
20 |
23 |
| 61 |
58 |
45 |
42 |
21 |
24 |
3
|
26 |
| 44 |
63 |
60 |
1
|
28 |
19 |
22 |
9
|
| 57 |
52 |
41 |
46 |
35 |
10 |
25 |
4
|
| 40 |
47 |
36 |
53 |
18 |
29 |
8
|
11 |
| 51 |
56 |
49 |
34 |
37 |
14 |
5
|
30 |
| 48 |
39 |
54 |
17 |
32 |
7
|
12 |
15 |
| 55 |
50 |
33 |
38 |
13 |
16 |
31 |
6
|
|
|
Fig 2
|
The Farmers puzzle:
Consider a farmer standing on the bank of a river with a dog, a sack of wheat and a goose. He wishes to transport these three and himself to the far bank by using a boat that will hold, at any one time, himself and at most one of his possessions. For obvious reasons, the goose cannot be left alone with the dog or the wheat. The puzzle is concerned with devising a sequence of crossings which allows the farmer to safely transport his possessions to the other bank. Using Graph Theory we can show that there are only two different ways. One way is :
1. Transport goose
2. Return empty
3. Transport wheat
4. Return with goose
5. Transport dog
6. Return empty
7. Transport goose.
Copyright © 2022 ICICI Centre for Mathematical Sciences
All rights reserved. Send us your suggestions at
|