|

ACOUSTICS OF THE INDIAN DRUM
Have you ever been disturbed by a child banging on a simple drum? Contrast this with the sound of a tabla or mridangam. Why is it that certain kinds of drums can produce melodious sounds and be tuned to specific notes while others cannot?
When we hear sounds, our eardrums pick up the alternate compressions and rarefactions of air produced by the vibrations of the source. For this sound to be musical, it must possess two characteristics: Pitch and Timbre.
Pitch: The pitch of a musical note is determined by its frequency. Frequency is the rate at which a waveform repeats itself and is measured in cycles per second (Hz).
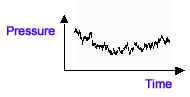 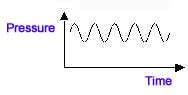
Periodic Waveform (sine wave) Non-periodic Waveform
For the sensation of pitch, the essential requirement is for the waveform to be periodic. A non-periodic waveform will not give the sensation of pitch.
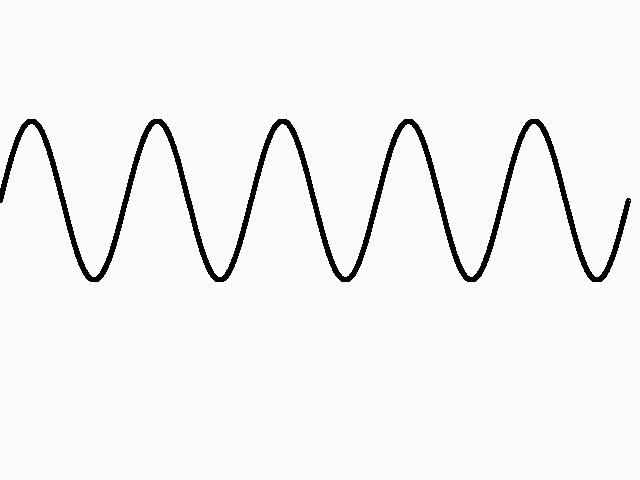
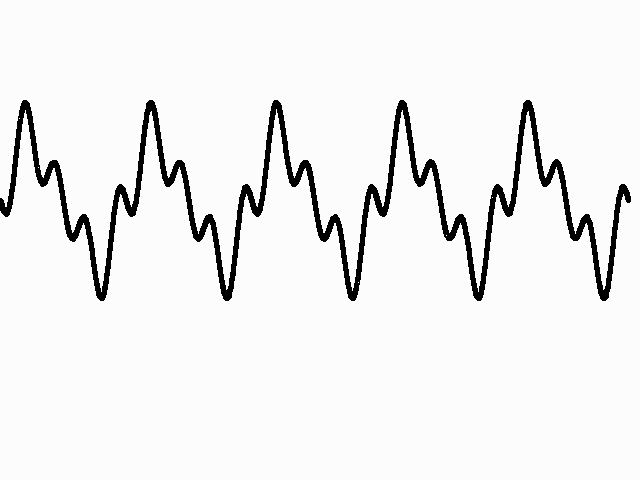
Timbre: Timbre refers to the quality of the sound. A tuning fork, a flute, a saxophone and a clarinet may all have the same pitch, but the timbre of each instrument is very different. While pitch depends on the frequency at which a waveform repeats itself, timbre depends on the shape of the waveform. Shown below are the waveforms of different instruments. They all have the same pitch but their timbres are very different.
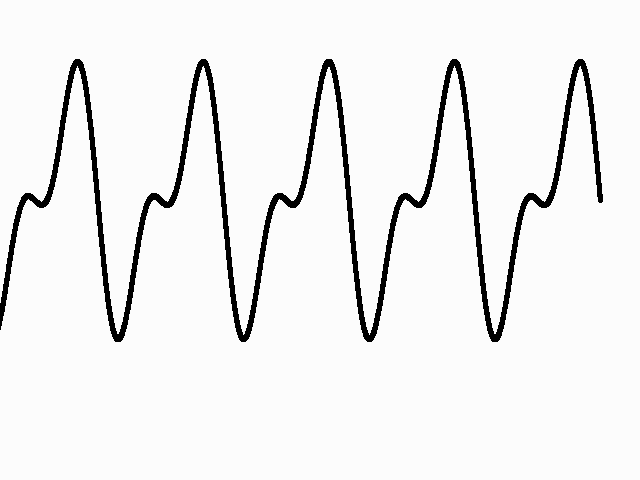
Tuning Fork (sine wave)
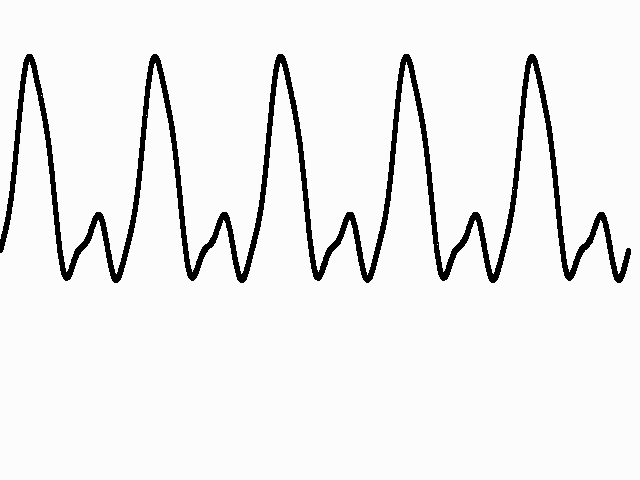
Saxophone
|
Flute
Clarinet
|
Overtones & Harmonics
The complex waveforms shown above are actually superpositions of sine waves of different frequencies. Notes produced by musical instruments consist of sine waves of one fundamental frequency and of higher frequencies called overtones. For the resultant waveform to be periodic, the overtones have to be integral multiples of the fundamental frequency (if the fundamental frequency is 240Hz, then the overtones should have frequencies 480Hz, 720Hz&). Overtones that are integral multiples of the fundamental frequency are called harmonics. Unless a majority of the overtones are harmonic, the wave will not be periodic and will not have a discernable pitch. Thus for a note to sound pleasing to the ear (musical), the overtones have to be harmonic.
Indian and Western Drums
The key difference between Indian and Western drums is that the membranes of Indian drums are loaded at the centre whereas the membranes of Western drums are uniform. The overtones produced by the uniform membranes of western drums are not harmonic. Loading the membranes suitably can make the drums harmonic.
The simple drum is a circular membrane with density r. When the membrane is set into oscillation, any point on it has a vertical displacement u(r, q, t), which is a function of the position (r, q) of the point P, at a time t. (See figure 1.) In other words u determines the shape of the membrane at any time.
Mathematically speaking, u is a solution of a wave equation that describes the vibration of the membrane. For a uniform membrane, the equation is the classical wave equation and can be solved exactly. On the other hand, when the density is not uniform, the equation has to be solved numerically on a computer.
Solution of the Wave equation
The solution u is the product of three functions: the radial solution, the theta solution and the time solution.
u(r, q, t) = R(r) × Q(q) × T(t)
The R solution: This describes how the displacement u of the membrane changes as one moves from the centre of the membrane outwards, along a radius. We shall see that there are certain circles on the membrane that remain stationary even when the drum vibrates. These are called Nodal Circles. These correspond to values of r for which R(r) reduces to zero. The R solution is given by
R(r) = Jn(kr) where Jn is the Bessel function of order n
As a mathematical description of the solution can get quite tedious, it has been described at the end. We have, however plotted (see figure 2) J0, J1 and J2 to give you an idea of what the Bessel functions look like. You will note that the zeros of the function are not equally spaced. The significance of this fact will be developed later.
Figure 2 (Bessel Functions)
k is called the wave number and is related to the frequency of the wave by the relation k = 2pf/c, where c is the speed of the wave and f is the frequency of the wave.
The q solution: This tells us how u changes with angle, i.e., how the displacement changes as we move along a circular path of fixed radius. There are certain values of q for which Q(q) reduces to zero. Thus, u would at all times be equal to zero on all diameters along which nq is an integral multiple of p/2. Nodal diameters of a drum are those diameters on the membrane that remain stationary while the drum is vibrating. There are n equally spaced nodal diameters where n is the order of the Bessel function. The solution is Q(q) = cos(nq).
The T Solution: This tells us how the displacement of a particular point of the membrane changes with time. The T solution shows that the membrane oscillates in time. The frequency of this wave is determined by the boundary conditions. The T solution is T(t) = cos(2pft)
Boundary Condition
The boundary of the membrane is fixed and cannot vibrate. This implies that at r = a, for all values of t and q (i.e. at all times and at all points on the circumference of the membrane), u should be 0. This can happen only when r = a coincides with one of the zeros of the Bessel function. Therefore, Jn (ka) = 0. This immediately restricts the values of k. If vnm are the values of ka at which the Bessel functions become 0, then k = vnm/a. Since values of vnm do not bear a simple ratio to each other (see figure 2), it follows immediately that the various frequencies present are not harmonic. Thus, the simple drum produces a non-musical sound.
Normal Modes Of Vibration
There are certain modes of vibration of the membrane that produce sine waves (remember the tuning fork). These are called normal modes of vibration. Each normal mode produces either the fundamental frequency or one of the overtones. When the membrane is struck, the resultant sound is more complex than that of a single normal mode, but may be considered as a superposition of normal modes.
For an instrument to be musical the frequencies associated with the normal modes must be multiples of the fundamental frequency. The normal modes of vibration of a drum are given below. (Please refer to the computer simulation).
Each normal mode is composed of various combinations of nodal diameters and circles and can be labelled as (a, b) where a is the number of nodal diameters and b is the number of nodal circles. The frequency associated with each mode (as a multiple of the fundamental) is given in blue. It can be seen that they are not harmonic.
Making the Drum Harmonic
We thus see that a membrane with uniform density fails to produce harmonics. To make a harmonic drum, we have to vary the density across the membrane; i.e. we have to load the membrane. In the tabla and mridangam, the first 9 normal modes produce the first 5 harmonics. Taking a cue from the right tabla drum, we experimented with various loading distributions. These were of two types:
1. Continuous loading: The density of the drum is specified as a continuous function of the normalized radius (r). The function used is:
r = 35(loge(0.68-r) +½loge(0.0612)½) for 0 < r < 0.62
r = 30 exp(1.2 r) for 0.93 < r < 1
r = 1 for 0.62 < r < 0.93
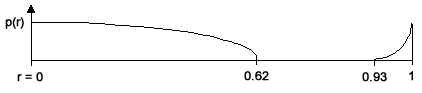
2. Multiple ring loading: The membrane is divided into concentric rings of different densities. With this technique we were able to make the first 11 normal modes harmonic. The density distribution is given below.
0.0 < r < 0.1 r = 6.896
0.1 < r < 0. r =11.692
0.2 < r < 0. r = 8.236
0.3 < r < 0. r = 9.228
0.4 < r < 0. r = 1.000
0.9 < r > 1. r = 2.664
r is the density of the membrane.
The radius of the membrane has been normalised to unity (a=1).
The equation for the loaded membrane was solved numerically on a computer for various loading distributions.
The above distributions were found to give good results. These are shown in table 1.
|
Normal
Mode
(diam, circ)
|
Frequency
(as a multiple of the fundamental)
|
|
Unloaded
Membrane
|
Multiple
Rings
|
Continuous
Loading
|
Tabla and
Mridangam
(approximate)
|
|
1 (0,0)
2 (1,0)
3 (2,0)
4 (0,1)
5 (3,0)
6 (1,1)
7 (4,0)
8 (2,1)
9 (0,2)
10 (1,2)
11 (1,3)
12 (2,2)
13 (3,1)
14 (4,1)
|
1.00
1.59
3.14
2.30
3.65
2.92
3.16
3.50
3.60
4.24
5.55
4.85
4.06
4.60
|
1.00
1.96
2.98
3.03
4.02
3.95
5.02
5.00
4.80
5.20
7.03
5.90
6.02
7.05
|
1.07
2.00
2.98
2.99
4.00
4.00
5.01
5.01
5.02
6.02
-
7.00
6.04
7.09
|
1
2
3
3
4
4
5
5
5
-
-
-
-
-
|
Table 1
Thus, we were able to determine a method of loading for a circular membrane in such a way that the first 14 normal modes would produce the first 7 harmonics. We shall now describe the mathematics involved.
The Wave Equation
A wave is mathematically represented by a wave equation. A wave equation relates the way in which the wave varies in time with the way in which the wave varies in space. The general form of the wave equation in polar coordinates is:
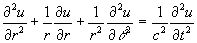
where c2 = t / r and c is the speed at which the wave travels, t is the tension in the membrane and r is the density of the membrane.
This equation is solved by the method of separation of variables. We assume that u(r, q, t) is a product of three functions R(r), Q(q) and T(t), each a function of only one variable. We get three separate equations:
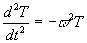 ------- 1 ------- 1
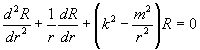 , k = w/c -------- 2 , k = w/c -------- 2
 And -------- 3 And -------- 3
Equations 1 and 3 are the differential equations representing Simple Harmonic Motion and have the sinusoidal solutions
T(t) = a1 sin(wt) + a2cos(wt)
And Q(t) = b1sin(mq) + b2cos(mq)
Equation 2 is called the Bessel Equation of order m and has the solution
R(r) = Jm(kr) where Jm is the Bessel Function of order m.
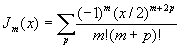 The Bessel function is actually an infinite power series: The Bessel function is actually an infinite power series:
The first few Bessel functions are plotted in figure 2, board 2. When the membrane is loaded symmetrically, the Q and T solutions remain the same. However the radial equation changes to
 -------- 4 -------- 4
For the uniform membrane (Eq 2), the permitted values of w, the angular frequency, are not integral multiples of each other. Hence the uniform membrane does not produce harmonics. In the case of the loaded membrane (Eq 4), the term k2 has been replaced by w2r(r)/t. By varying r(r), we can make the allowed values of w integral multiples of each other.
Equation 4 was solved numerically using the 2nd order Runge-Kutta method to find the values of w that satisfied the boundary conditions. The functions r(r) that gave harmonics have been described in this project.
Copyright © 2022 ICICI Centre for Mathematical Sciences
All rights reserved. Send us your suggestions at
|